26.2. K-Means Clustering: A Larger Example#
Now that we understand the k-means clustering algorithm, let’s try an example with more features and use and elbow plot to choose \(k\). We will also show how you can (and should!) run the algorithm multiple times with different initial centroids because, as we saw in the animations from the previous section, the initialization can have an effect on the final clustering.
Clustering Countries#
For this example, we will use a dataset[1] with information about countries across the world. It includes demographic, economic, environmental, and socio-economic information from 2023. This data and more information about it can be found here. The first few lines are shown below.
countries = pd.read_csv("../../data/world-data-2023.csv")
countries.head()
| Country | Density\n(P/Km2) | Abbreviation | Agricultural Land( %) | Land Area(Km2) | Armed Forces size | Birth Rate | Calling Code | Capital/Major City | Co2-Emissions | ... | Out of pocket health expenditure | Physicians per thousand | Population | Population: Labor force participation (%) | Tax revenue (%) | Total tax rate | Unemployment rate | Urban_population | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Afghanistan | 60 | AF | 58.10% | 652,230 | 323,000 | 32.49 | 93.0 | Kabul | 8,672 | ... | 78.40% | 0.28 | 38,041,754 | 48.90% | 9.30% | 71.40% | 11.12% | 9,797,273 | 33.939110 | 67.709953 |
| 1 | Albania | 105 | AL | 43.10% | 28,748 | 9,000 | 11.78 | 355.0 | Tirana | 4,536 | ... | 56.90% | 1.20 | 2,854,191 | 55.70% | 18.60% | 36.60% | 12.33% | 1,747,593 | 41.153332 | 20.168331 |
| 2 | Algeria | 18 | DZ | 17.40% | 2,381,741 | 317,000 | 24.28 | 213.0 | Algiers | 150,006 | ... | 28.10% | 1.72 | 43,053,054 | 41.20% | 37.20% | 66.10% | 11.70% | 31,510,100 | 28.033886 | 1.659626 |
| 3 | Andorra | 164 | AD | 40.00% | 468 | NaN | 7.20 | 376.0 | Andorra la Vella | 469 | ... | 36.40% | 3.33 | 77,142 | NaN | NaN | NaN | NaN | 67,873 | 42.506285 | 1.521801 |
| 4 | Angola | 26 | AO | 47.50% | 1,246,700 | 117,000 | 40.73 | 244.0 | Luanda | 34,693 | ... | 33.40% | 0.21 | 31,825,295 | 77.50% | 9.20% | 49.10% | 6.89% | 21,061,025 | -11.202692 | 17.873887 |
5 rows × 35 columns
We want to see if we can cluster countries based on their characteristics. First, we need to do some cleaning. I don’t want to include Abbreviation, Calling Code, Capital/Major City, Largest city, Latitude, or Longitude in my analysis because they uniquely identify a given country. I also see some variables that are numeric with percentage signs, dollar signs, and commas. These are characters which indicate that the variable is a string, but I would like them to be floats instead so that Python knows they have a numerical meaning.
The code used for this cleaning is hidden for brevity, but the resulting, clean dataframe is shown below.
Show code cell source
countries_clean = countries.drop(columns = ['Abbreviation', 'Calling Code', 'Capital/Major City', 'Largest city', 'Latitude', 'Longitude','Minimum wage'])
def str_to_num(my_input):
'''Takes in a number in string format and removes commas
and percentage signs before returning it as a float or int
If the string is not a number or input is not a string,
returns the input'''
if type(my_input) is str:
cleaned_input = my_input.strip() #strip trailing whitespace
cleaned_input = cleaned_input.removeprefix("$").removesuffix("%") #remove these characters if they are present
if cleaned_input.isdigit():
return int(cleaned_input)
elif ("." in cleaned_input) and (cleaned_input.replace(".","").replace("-","").isdigit()): #is the only non-digit character a "."
return float(cleaned_input)
elif ("," in cleaned_input) and (cleaned_input.replace(",","").replace("-","").isdigit()): #is the only non-digit character a ","
return int(cleaned_input.replace(",",""))
elif ("." in cleaned_input) and ("," in cleaned_input) and (cleaned_input.replace(".","").replace(",","").replace("-","").isdigit()): #contains 2 non-digit characters "," and "."
return float(cleaned_input.replace(",",""))
else:
return my_input
else:
return my_input
countries_clean = countries_clean.map(str_to_num) #apply this function to every cell in the dataframe
countries_clean = countries_clean.dropna(subset=countries_clean.columns.difference(['Official language','Currency code']),ignore_index = True) #remove rows with any missing numeric values
countries_clean.head()
| Country | Density\n(P/Km2) | Agricultural Land( %) | Land Area(Km2) | Armed Forces size | Birth Rate | Co2-Emissions | CPI | CPI Change (%) | Currency-Code | ... | Maternal mortality ratio | Official language | Out of pocket health expenditure | Physicians per thousand | Population | Population: Labor force participation (%) | Tax revenue (%) | Total tax rate | Unemployment rate | Urban_population | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Afghanistan | 60 | 58.1 | 652230.0 | 323000.0 | 32.49 | 8672.0 | 149.90 | 2.3 | AFN | ... | 638.0 | Pashto | 78.4 | 0.28 | 38041754.0 | 48.9 | 9.3 | 71.4 | 11.12 | 9797273.0 |
| 1 | Albania | 105 | 43.1 | 28748.0 | 9000.0 | 11.78 | 4536.0 | 119.05 | 1.4 | ALL | ... | 15.0 | Albanian | 56.9 | 1.20 | 2854191.0 | 55.7 | 18.6 | 36.6 | 12.33 | 1747593.0 |
| 2 | Algeria | 18 | 17.4 | 2381741.0 | 317000.0 | 24.28 | 150006.0 | 151.36 | 2.0 | DZD | ... | 112.0 | Arabic | 28.1 | 1.72 | 43053054.0 | 41.2 | 37.2 | 66.1 | 11.70 | 31510100.0 |
| 3 | Angola | 26 | 47.5 | 1246700.0 | 117000.0 | 40.73 | 34693.0 | 261.73 | 17.1 | AOA | ... | 241.0 | Portuguese | 33.4 | 0.21 | 31825295.0 | 77.5 | 9.2 | 49.1 | 6.89 | 21061025.0 |
| 4 | Argentina | 17 | 54.3 | 2780400.0 | 105000.0 | 17.02 | 201348.0 | 232.75 | 53.5 | ARS | ... | 39.0 | Spanish | 17.6 | 3.96 | 44938712.0 | 61.3 | 10.1 | 106.3 | 9.79 | 41339571.0 |
5 rows × 28 columns
Preprocessing the Data#
In the previous section, we wrote our own functions to implement the k-means algorithm. This is a useful exercise to make sure we understand how the algorithm works, but as we know, there are libraries with optimized functions built to do these kinds of common analyses. The library sklearn has built-in functions to do k-means clustering that are much faster than the functions we wrote. Let’s use these functions to cluster our countries dataset.
Before, we can cluster the data, we need to do some preprocessing. Below, I import StandardScaler which we can use to standardize our data.
from sklearn.preprocessing import StandardScaler
Next, we separate our numeric and categorical data for ease of preprocessing.
country_names = countries_clean['Country']
num_columns = countries_clean.drop(columns=['Country', 'Currency-Code', 'Official language'])
cat_columns = countries_clean[['Currency-Code', 'Official language']]
Now, we can use get_dummies from the pandas library to dummy code our categorical features. I set drop_first equal to True so that the first category will be dropped and used as the reference level. I also set dummy_na equal to True which creates a dummy variable to indicate which values are missing.
cat_dummies = pd.get_dummies(cat_columns, drop_first=True, dummy_na=True)
Next, we need to initialize our StandardScaler and use it to scale our numeric features.
scaler = StandardScaler()
num_scaled = pd.DataFrame(scaler.fit_transform(num_columns),columns=num_columns.columns)
Now, we can put our categorical and numerical data back together into one preprocessed dataframe using the .concat function from pandas.
countries_proc = pd.concat([num_scaled,cat_dummies], axis = 1)
countries_proc.head()
| Density\n(P/Km2) | Agricultural Land( %) | Land Area(Km2) | Armed Forces size | Birth Rate | Co2-Emissions | CPI | CPI Change (%) | Fertility Rate | Forested Area (%) | ... | Official language_Swahili | Official language_Swedish | Official language_Tamil | Official language_Thai | Official language_Tok Pisin | Official language_Turkish | Official language_Ukrainian | Official language_Urdu | Official language_Vietnamese | Official language_nan | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.215644 | 0.818138 | -0.115866 | 0.348798 | 1.264388 | -0.232539 | -0.077214 | -0.280488 | 1.414957 | -1.256779 | ... | False | False | False | False | False | False | False | False | False | False |
| 1 | -0.156441 | 0.115295 | -0.389922 | -0.417215 | -0.788460 | -0.236728 | -0.335232 | -0.389776 | -0.774075 | -0.051855 | ... | False | False | False | False | False | False | False | False | False | False |
| 2 | -0.270901 | -1.088910 | 0.644351 | 0.334160 | 0.450584 | -0.089375 | -0.065003 | -0.316917 | 0.301239 | -1.317025 | ... | False | False | False | False | False | False | False | False | False | False |
| 3 | -0.260376 | 0.321462 | 0.145437 | -0.153746 | 2.081166 | -0.206181 | 0.858093 | 1.516694 | 2.221443 | 0.791591 | ... | False | False | False | False | False | False | False | False | False | False |
| 4 | -0.272217 | 0.640084 | 0.819584 | -0.183020 | -0.269053 | -0.037369 | 0.615715 | 5.936791 | -0.282503 | -0.899936 | ... | False | False | False | False | False | False | False | False | False | False |
5 rows × 192 columns
Choosing K#
Now that our data has been preprocessed, we are ready to start clustering. First, we import the KMeans function from sklearn.cluster.
from sklearn.cluster import KMeans
The KMeans function takes in the number of clusters, \(k\), as n_clusters, the number of times the algorithm should be run with different initial centroids as n_init, and a random seed (as explained in Section 10.3) as random_state. It also takes in a maximum number of iterations and a tolerance as max_iter with default 300 and tol with default \(10^{-4}\) respectively. For more information about the function, see the scikit-learn documentation here.
As we mentioned in the previous section, when it is not obvious how many clusters to use, we can build an Elbow Plot to help us choose \(k\). Below, we use iteration to try different values (here 1-10) for \(k\). For each \(k\) we try, we initialize our KMeans() function with that \(k\) value and set n_init to 10 which tries 10 different initial random centroids and chooses the resulting clustering with the smallest WCV. We fit this model to countries_proc and save the WCV which can be found using the attribute .inertia_. The for loop below results in a list of WCV values which we can use to build our elbow plot.
wcv = []
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, n_init=10)
kmeans.fit(countries_proc)
wcv.append(kmeans.inertia_)
plt.plot(range(1, 11),wcv)
plt.xlabel("Number of Clusters: k")
plt.ylabel("Within-Cluster Variation")
plt.title('Elbow Plot for Choosing Number of Country Clusters');
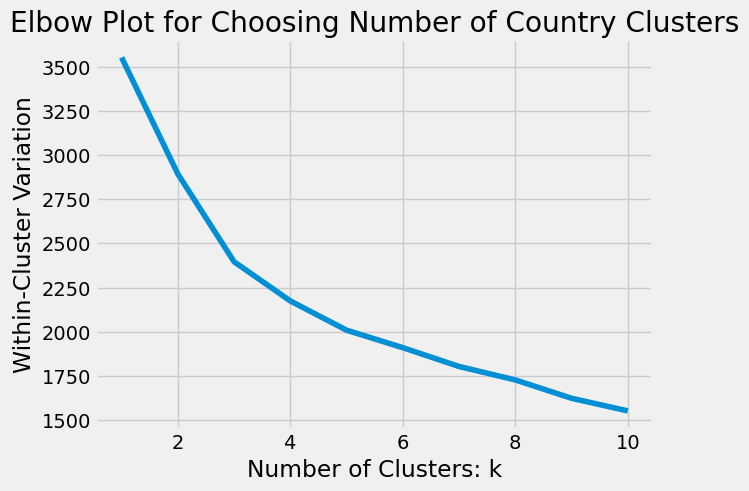
The elbow of this plot is not as clear as the plot from the previous section. It looks to be somewhere between 3 and 5. We will choose \(k = 4\) clusters for our data, since 4 is in the middle.
Training Our Model#
Now that we have chosen k, we can use KMeans to cluster our dataset into 4 clusters. The attribute .labels_ shows us the cluster membership for each row of countries proc.
kmeans = KMeans(n_clusters=4, n_init=10)
kmeans.fit(countries_proc)
kmeans.labels_
array([0, 2, 1, 0, 1, 1, 2, 2, 1, 1, 1, 2, 2, 2, 0, 1, 1, 2, 0, 0, 0, 1,
0, 2, 2, 3, 1, 0, 2, 2, 2, 2, 0, 2, 1, 1, 2, 0, 1, 2, 2, 0, 0, 2,
2, 0, 2, 1, 0, 1, 2, 2, 3, 1, 1, 1, 2, 2, 2, 2, 1, 1, 0, 1, 1, 0,
2, 1, 2, 2, 0, 0, 1, 0, 2, 2, 1, 1, 1, 1, 0, 1, 1, 2, 1, 0, 0, 2,
1, 1, 0, 1, 2, 1, 2, 2, 1, 2, 1, 0, 1, 0, 2, 0, 2, 2, 2, 1, 2, 2,
1, 0, 2, 2, 2, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 2, 3, 2, 1, 0],
dtype=int32)
We can investigate which countries were clustered together using the country_names data which we extracted from our original dataset.
Cluster 0 seems to contain mostly European countries.
country_names[kmeans.labels_ == 0]
0 Afghanistan
3 Angola
14 Benin
18 Burkina Faso
19 Burundi
20 Ivory Coast
22 Cameroon
27 Republic of the Congo
32 Democratic Republic of the Congo
37 Ethiopia
41 Gabon
42 The Gambia
45 Ghana
48 Guinea
62 Kenya
65 Laos
70 Madagascar
71 Malawi
73 Mali
80 Mozambique
85 Niger
86 Nigeria
90 Papua New Guinea
99 Rwanda
101 Senegal
103 Sierra Leone
111 Sudan
117 Tanzania
119 East Timor
120 Togo
124 Uganda
131 Zambia
Name: Country, dtype: object
Cluster 1 contains many Middle Eastern and Eastern European countries as well as Southern and Central American countries.
country_names[kmeans.labels_ == 1]
2 Algeria
4 Argentina
5 Armenia
8 Azerbaijan
9 Bahrain
10 Bangladesh
15 Botswana
16 Brazil
21 Cape Verde
26 Colombia
34 Dominican Republic
35 Egypt
38 Fiji
47 Guatemala
49 Honduras
53 Indonesia
54 Iran
55 Iraq
60 Jordan
61 Kazakhstan
63 Kuwait
64 Kyrgyzstan
67 Lebanon
72 Malaysia
76 Mexico
77 Moldova
78 Mongolia
79 Morocco
81 Myanmar
82 Nepal
84 Nicaragua
88 Oman
89 Pakistan
91 Paraguay
93 Philippines
96 Qatar
98 Russia
100 Saudi Arabia
107 South Africa
110 Sri Lanka
115 Syria
116 Tajikistan
118 Thailand
121 Trinidad and Tobago
122 Tunisia
123 Turkey
125 Ukraine
126 United Arab Emirates
130 Vietnam
Name: Country, dtype: object
Cluster 2 contains mostly African countries.
country_names[kmeans.labels_ == 2]
1 Albania
6 Australia
7 Austria
11 Barbados
12 Belgium
13 Belize
17 Bulgaria
23 Canada
24 Chile
28 Costa Rica
29 Croatia
30 Cyprus
31 Czech Republic
33 Denmark
36 Estonia
39 Finland
40 France
43 Georgia
44 Germany
46 Greece
50 Hungary
51 Iceland
56 Republic of Ireland
57 Israel
58 Italy
59 Jamaica
66 Latvia
68 Lithuania
69 Luxembourg
74 Malta
75 Mauritius
83 New Zealand
87 Norway
92 Peru
94 Poland
95 Portugal
97 Romania
102 Serbia
104 Singapore
105 Slovakia
106 Slovenia
108 South Korea
109 Spain
112 Suriname
113 Sweden
114 Switzerland
127 United Kingdom
129 Uruguay
Name: Country, dtype: object
China, India and the United States make up their own cluster.
country_names[kmeans.labels_ == 3]
25 China
52 India
128 United States
Name: Country, dtype: object
The map below shows which countries are assigned to each cluster. Interestingly, the clustering seems to have some geographic meaning. Countries close together on the map tend to belong to the same cluster.
Show code cell source
import plotly.express as px
dat = pd.DataFrame({'country_names': country_names, 'cluster': np.array([str(lab) for lab in kmeans.labels_])})
fig = px.choropleth(dat, locations="country_names",
locationmode='country names',
color="cluster",
color_discrete_sequence=["#D81B60","#1E88E5","#FFC107","#004D40"],
hover_name="country_names",
category_orders={"cluster":["0","1","2","3"]})
fig.update_layout(legend_title_text='Cluster Membership')
fig.show()
Disadvantages of K-Means Clustering#
As we discussed previously, k-means clustering has several disadvantages. It does not always converge to a solution that provides the global minimum within-cluster variation. Because of this, it can also give differing solutions depending on the initial starting points. In addition, the k-means algorithm requires the user to specify the number of clusters, which may not always be obvious, especially for data with high dimensionality. In the next section, we will discuss another clustering method that does not require you to specify a number of clusters: hierarchical clustering.
